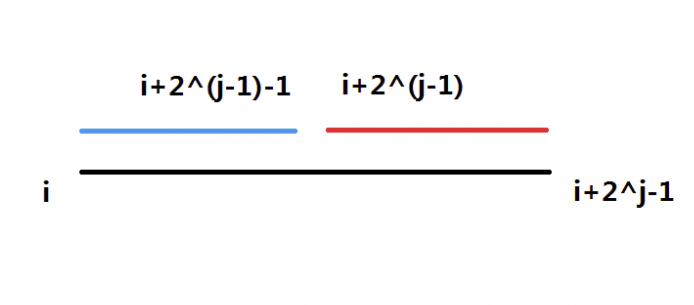ST 表

ST 表原理和模板代码

ST 表的目标 -RMQ 问题

简而言之，就是询问区间最值的问题

区间最值不具有区间可减性，不能用树状数组这样的数据结构来维护

ST 算法是 RMQ 问题的一个常用解法，使用了动态规划的思想。

1. 预处理数组 f[x][i] 表示区间 $[x,x+2^i)$ 的最值，其中
   $$f[x][i]=min/max(f[x][i-1],f[x+2^{i-1}][i-1])$$
2. 对于询问区间[l,r], 设 $d=log_2(r-l+1)$，答案即为 $min/max(f[l][d],f[r-2^d+1][d])$

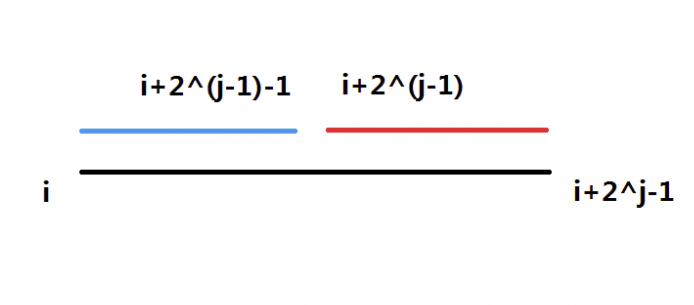
代码

const int maxn=1e5+50;
int n,m;
int f[maxn][18];

int que(int l,int r){
    int d=log2(r-l+1);
    return max(f[l][d],f[r-(1<<d)+1][d]);
}

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>f[i][0];
    for(int j=1;j<=17;j++){
        for(int i=1;i+(1<<(j-1))<=n;i++){
            f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
        }
    }

    for(int i=1,l,r;i<=m;i++){
        cin>>l>>r;
        cout<<que(l,r)<<'\n';
    }
}

ST 表 + 倍增法例题 leetcode1521

const int maxn=1e5+100;
int dp[maxn][21];

class Solution {
public:
    void init(int n){
        for(int j=1;j<=20;j++){
            for(int i=1;i+(1<<(j-1))<=n;i++){
                dp[i][j]=dp[i][j-1] & dp[i+(1<<(j-1))][j-1];
            }
        }
    }

    int query(int l,int r){
        if(l>r)return -1e7;
        int j=log2(r-l+1);
        return dp[l][j] & dp[r-(1<<j)+1][j];
    }

    int closestToTarget(vector<int>& arr, int target) {
        int n=arr.size();
        for(int i=1;i<=n;i++){
            dp[i][0]=arr[i-1];
        }
        init(n);

        int r,nr,ans=1e7;
        for(int l=1;l<=n;l++){
            r=l;
            for(int k=20;k>=0;k--){
                nr=l+(1<<k);
                if(nr>=n) continue;
                if(query(l,nr)>=target){
                    r=nr;
                    break;
                }
            }
            ans=min(ans,abs(target-query(l,r)));
            if(r+1<=n) ans=min(ans,abs(target-query(l,r+1)));
        }
        return ans;
    }
};