树状数组

树状数组原理和模板代码

树状数组的目标 - 动态前缀和问题

1. 求数列 [1,r] 元素的和，即 $\sum^{r}_{i=1}{a_i}$ 的值
2. 修改 ${a_x}$ 的值为 v

lowbit 操作

lowbit(x)=-x&x

树状数组定义

1. 令第 i 个位置记录（i-lowbit(i),i]中的数字的和
2. 令第 i 个位置的父节点为 i+lowbit(i)

性质：

1. 一个节点 i，记录区间（i-lowbit(i),i]的信息，其子节点记录的区间不会相互覆盖，且按照由小到大依次覆盖区间(i-lowbit(i),i)

2. 一个位置 i，仅会被节点 i 及其祖先节点覆盖

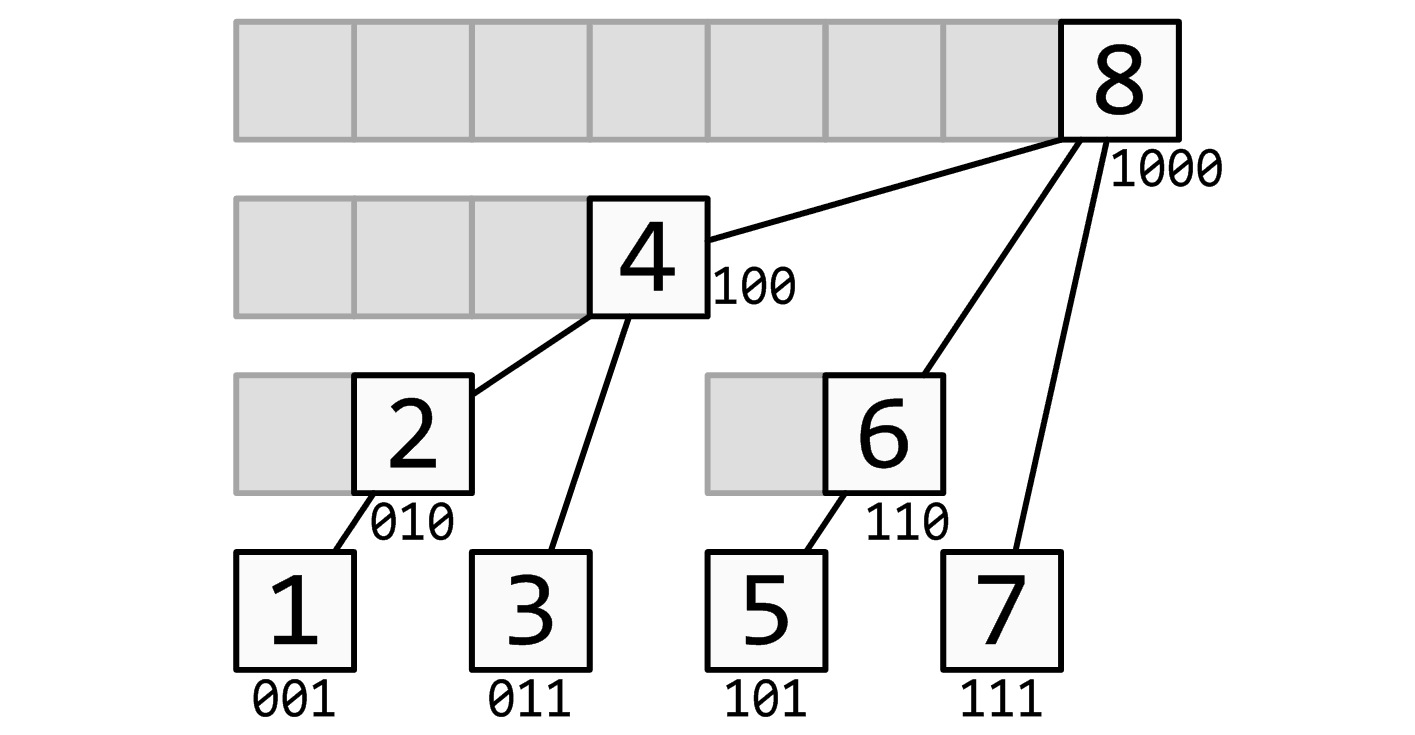
代码

更新操作

void update(int x,int y){
    while(x<=n) d[x]+=y,x+=lowbit(x);
}

查询操作

int ask(int r){
    int res=0;
    while(r) res+=d[r],r-=lowbit(r);
    return res;
}

树状数组经典应用 - 求逆序对个数

遍历数组，遍历过程中 ans+=ask(MAX)-ask(a[i])
同时更新update(a[i],1)

输入数组到 a[n]，如 [5,4,2,6,3,1]

for(int i=0;i<=n;i++){
    res+=ask(MAX)-ask(a[i]);
    update(da[i],1);
}

 输出答案 res